10157. Transitive closure

Find the transitive closure of the directed graph.

Input. The directed graph is given with the list of edges. The first line contains the number of vertices n (1 ≤ n ≤ 100). Each of the next lines contains two vertices a and b (1 ≤ a, b ≤ n) describing the directed edge from a to b.

Output. Print the adjacency matrix of the transitive closure of the directed graph.

Sample input	Sample output
4 4 1 1 2 3 4	0 1 0 0 0 0 0 0 1 1 0 1 1 1 0 0

SOLUTION

transitive closure of the graph

Algorithm analysis

In the problem you must find the transitive closure of the graph. If graph contains the edges i → k and k → j, the edge i → j should be added.

Example

Consider the graph at the left. Its transitive closure is given at the right.

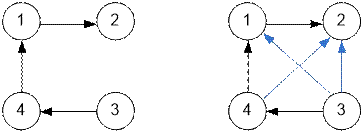
In the transitive closure the next edges will be added: 3 → 1 (there is a path 3 → 4 → 1), 3 → 2 (path 3 → 4 → 1 → 2) and 4 → 2 (path 4 → 1 → 2).

Algorithm realization

Declare adjacency matrix g.

#define MAX 101

bool g[MAX][MAX];

Read the input data. Create the graph.

scanf("%d", &n);

while (scanf("%d %d", &a, &b) == 2)

g[a][b] = true;

Start the transitive closure algorithm. If there are edges i → k and k → j, then create an edge i → j.

for (k = 1; k <= n; k++)

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

if (g[i][k] && g[k][j]) g[i][j] = true;

Print the adjacency matrix of transitive closure of the graph.

for (i = 1; i <= n; i++)

{

for (j = 1; j <= n; j++)

printf("%d ", g[i][j]);

printf("\n");

}

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

boolean g[][] = new boolean[n+1][n+1];

while (con.hasNextInt())

{

int a = con.nextInt();

int b = con.nextInt();

g[a][b] = true;

}

for (int k = 1; k <= n; k++)

for (int i = 1; i <= n; i++)

for (int j = 1; j <= n; j++)

if (g[i][k] && g[k][j]) g[i][j] = true;

for (int i = 1; i <= n; i++)

{

for (int j = 1; j <= n; j++)

{

int val = (g[i][j]) ? 1 : 0;

System.out.print(val + " ");

}

System.out.println();

}

con.close();

}

}